Floquet description of NMR experiments
Many solid-state NMR experiments exploit interference effects between various time dependencies in the system Hamiltonian to design an effective time-independent Hamiltonian with the desired properties. Effective Hamiltonians can be engineered such that they contain only selected parts of the full system Hamiltonian, while all other parts are averaged to zero. A general theoretical description of such experiments has to accommodate several time-dependent perturbations with incommensurate frequencies.
Over the past years we have formalyzed analytical operator-based Floquet description of NMR experiments for situations with two, three, and four incommensurate frequencies. The Floquet description is general in the sense that the resulting effective Hamiltonians can be calculated without a detailed knowledge of the spin-system Hamiltonian and can be fully expressed as a function of the Fourier components of the time-dependent Hamiltonian.
We use a Floquet description to analyze existing experiments and engineer new ones, e.g. novel decoupling and recoupling schemes. Analyzing such experiments by using average Hamiltonian theory requires additional assumptions that can be avoided by using Floquet theory.
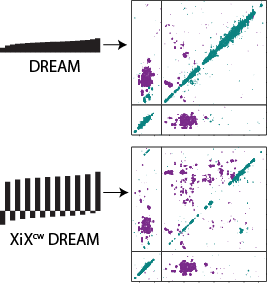
For instance, we have developed the XiXCW DREAM recoupling pulse sequence, a more broad-banded version of the DREAM double-quantum dipolar-recoupling sequence. The recoupling conditions and the corresponding first-order effective Hamiltonian have been analyzed using triple-mode Floquet theory.
Collaboration with external page P. K. Madhu (TIFR Mumbai, India) and Anders B. Nielsen (Aarhus University, Denmark).